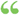 If the square described on one side of a triangle be equal to the sum of the squares described on the other two sides, the angle contained by these two sides is a right angle. If the square described on one side of a triangle be equal to the sum of the squares described on the other two sides, the angle contained by these two sides is a right angle.  Reports on Elementary schools - Page 810by Her MAjesty' Inspectors of schools - 1850Full view Reports on Elementary schools - Page 810by Her MAjesty' Inspectors of schools - 1850Full view - About this book
 | Euclides - 1821 - 294 pages
...side is the same.. For it is the O2 of the perpendicular. ,. • PROP. 48. TIIEOR. Jf the square of one side of a triangle be equal to the sum of the squares of the other troo sides, the angle opposite to that side is a right angle. From the vertex of this... | |
 | George Lees - 1826 - 276 pages
...triangle, SeC. QED Cor. If the square described upon one of the sides of a triangle, be equivalent to the sum of the squares described upon the other two sides, the angle contained by these twq sides is a right angle. ELEMENTS OF GEOMETRY. BOOK II. DEFINITIONS.... | |
 | George Darley - Geometry - 1828 - 190 pages
...calculations ; which calculations, however, depend on the principles of Geometry and Trigonometry. AHT. 132. " If the square described upon one side of a triangle be equal to the squares described on the other sides of the triangle, taken together, the angle opposite to thejirstmentioned... | |
 | Timothy Walker - Geometry - 1829 - 156 pages
...polygon. 108. THEOKEM. — The square described upon the hypothenuse of a right triangle is equivalent to the sum of the squares described upon the other two sides. This is the celebrated proposition, with the discovery of which Pythagoras is said to have been so... | |
 | James Hayward - Geometry - 1829 - 218 pages
...c8, that is — The square described upon the hypothenuse of a right-angled triangle, is equivalent to the sum of the squares described upon the other two sides. 173. We may demonstrate this truth from the areas immediately, without referring the lines to numbers,... | |
 | Pierce Morton - Geometry - 1830 - 584 pages
...to the turn of the squares of the sides which contain that angle : and conversely, if the square of one side of a triangle be equal to the sum of the squares of the other two sides, the angle contained by these two sides shall be a right angle. Let AB С be... | |
 | John Martin Frederick Wright - Astronomy - 1831 - 282 pages
...cycloid. TRINITY COLLEGE, MAY 1828. 1 . IP the square described upon one of the sides of a triangle is equal to the sum of the squares described upon the other two ; the angle contained by these two is a right angle. 2. In a given circle to inscribe a triangle equiangular... | |
 | Euclid - Euclid's Elements - 1833 - 216 pages
...Fig. 71. PROP. XLVIII. THEOR. Fig. 72. If the square described upon one side (AC] of a triangle (ABC) be equal to the sum of the squares described upon the other two sides (AB andBC), the angle (ABC) opposite to that side is a right angle. 1 i ) SchoL From the point B draw... | |
 | Thomas Perronet Thompson - Euclid's Elements - 1833 - 168 pages
...was to be demonstrated. PROPOSITION XLVIII. THEOREM. — If the square described on one of the sides of a triangle, be equal to the sum of the squares described on the other two sides of it; the angle made by those two sides is a right angle. Let ABC be a triangle,... | |
 | Mathematics - 1835 - 684 pages
...to the sum of the squares of the sides which contain that angle : and conversely, if the square of one side of a triangle be equal to the sum of the squares of the other two sides, the angle contained by those two sides shall be a right angle. Let ABC be a... | |
| |